Current Research
Some of the problems I am working on
Regularity of infinitely degenerate elliptic equations.
We implement the De Giorgi iteration method to weak solutions of infinitely degenerate elliptic operators. We developed an abstract theory with sufficient conditions for boundedness of solutions, as well as sufficient conditions for continuity of solutions. We apply this abstract theory to the highly degenerate geometry induced by some model operators in two and higher dimensions and obtain new a-priori results for the corresponding weak solutions.
Currently, I am working in refining this method, and obtain a tighter proof in terms of Orlicz norms.

Kato type estimates for the weight heat semigroup
We extend techniques developed by Auscher-Egert-Nystrom to weighted elliptic operators.
Paper in preparation.
Applied Differential Equations
I am always open to work, mentor, or collaborate on applied mathematics problems. I have always been fascinated with physics and scientific discovery, and I learned computer programming at a young age. My first university degree is in applied mathematics.
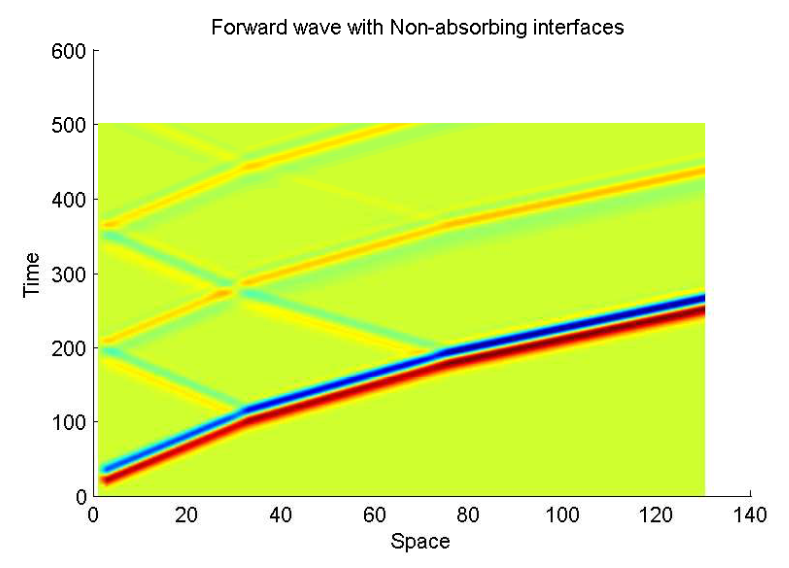
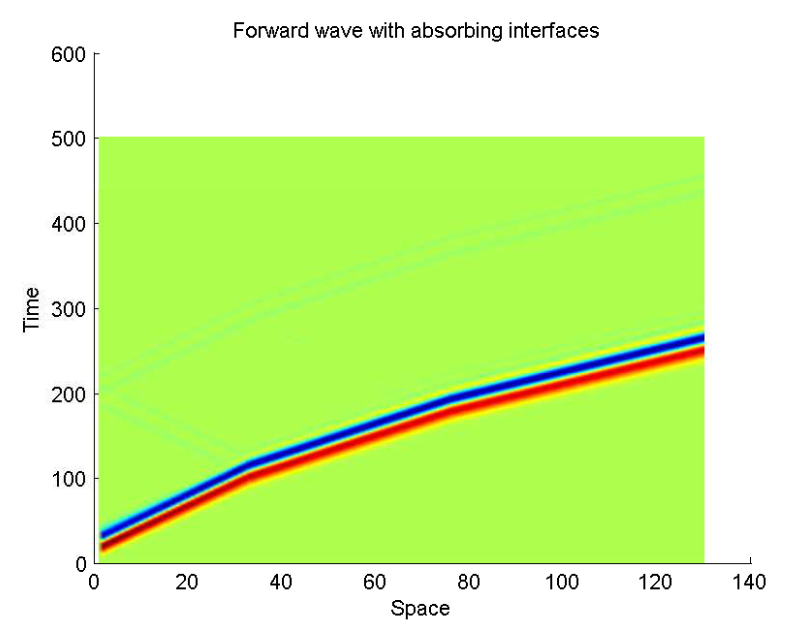
I supervised a Ph.D. dissertation on inversion problems related to imaging the densities of the Earth subsurface via analysis of seismic waves. We concentrated on diminishing the effect of artificial boundary conditions necessary for numerical implementation of solutions.
Currently I am supervising Ph.D. research related to machine learning algorithms. We are analyzing the effects of regularization in the optimization cost function.